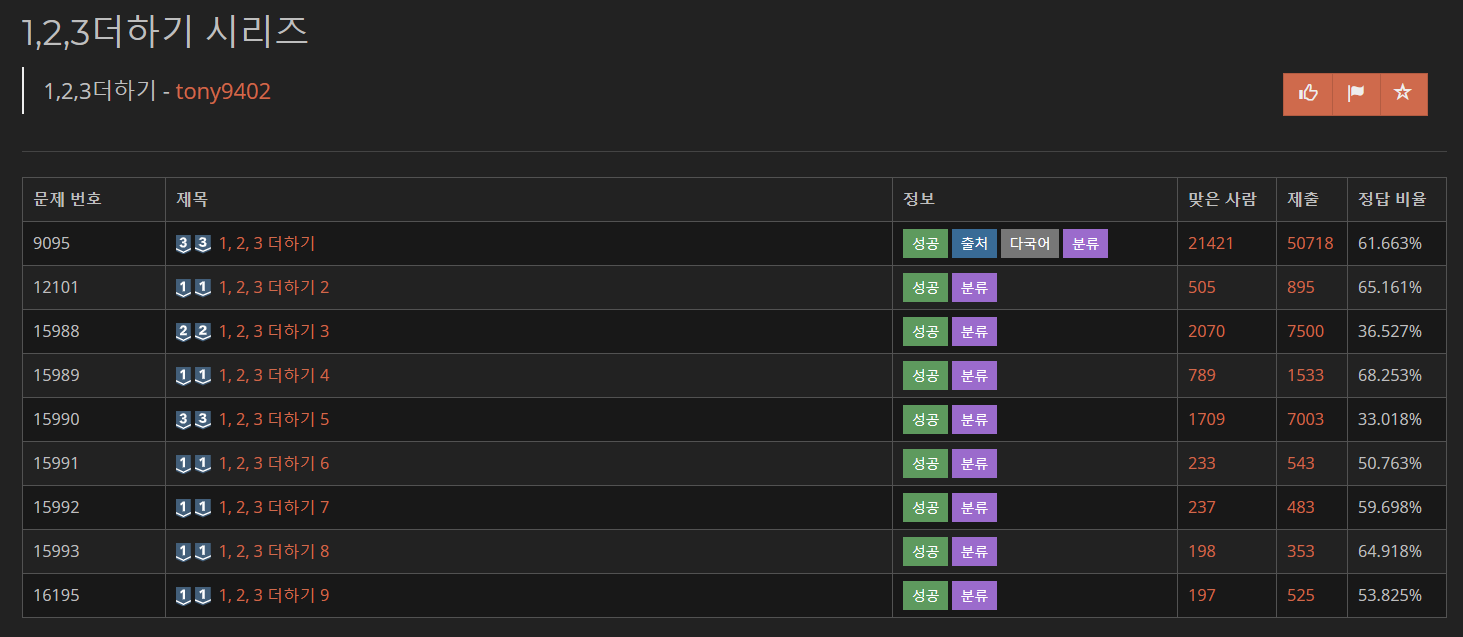
tony9402라는 분이 문제집을 잘 만들어두셔서, 그대로 첨부한다.
www.acmicpc.net/workbook/view/2154
문제집: 1,2,3더하기 시리즈 (tony9402)
www.acmicpc.net
문제들은 전반적으로 쉽다. 실버 문제들이니까?
주 문제 상황은 어떤 수 N을 1, 2, 3의 합으로 나타내는 경우의 수를 구하는 것이다.
주로 사용한 아이디어는 DP이다.
차례대로 풀이해보자.
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
그냥 D[i] = i를 1, 2, 3을 이용해 나타낸 경우의 수(순서 고려 O) 라고, 정의한다면
D[i] = D[i-1] + D[i-2] + D[i-3]로 풀 수 있다.
12101번: 1, 2, 3 더하기 2
n을 1, 2, 3의 합으로 나타내는 방법 중에서 사전 순으로 k번째에 오는 것을 출력한다. k번째 오는 식이 없는 경우에는 -1을 출력한다.
www.acmicpc.net
M은 무지막지하게 커보여서 겁 먹을 수도 있다.
하지만 N이 11이므로, 그냥 dfs로 완전탐색을 돌리면 된다.
15988번: 1, 2, 3 더하기 3
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다.
www.acmicpc.net
문제 1번과 동일하다, 1번을 DP로 풀어버려서 동일하게 해결할 수 있다. 단지 MOD 처리만 추가하면 된다.
15989번: 1, 2, 3 더하기 4
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 4가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다. 합을 이루고 있는 수의 순서만 다른 것은 같은 것으로 친다. 1+1+1+1 2+1+1 (1+1+2, 1+2+1) 2+2
www.acmicpc.net
이 문제는 숫자의 조합이 같으면 같은 경우의 수로 생각하기 때문에 조금 특이하게 생각하고 풀었다.
최대 범위가 10,000인데, 어떤 수든 그러면 3을 최대 3333개 사용할 수 있다.
근데, 3의 사용 횟수를 정해놓으면 2와 1에 따른 경우의 수는 다음과 같다. (N - 3*k) // 2 + 1, k = 3의 사용 횟수
(한번 숫자들을 나열해보면 알 듯 하다.)
아무튼 이런 식으로 하면 하나의 N에 대해서 최대 3333번의 연산을 하므로 TLE 받지않고 넘길 수 있다.
15990번: 1, 2, 3 더하기 5
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다.
www.acmicpc.net
D[i][j] = i라는 숫자를 만드는 데, 맨 마지막에 j(1~3)를 사용한 경우의 수
라고 DP 배열을 정의하고 풀면 된다.
15991번: 1, 2, 3 더하기 6
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다.
www.acmicpc.net
숫자가 대칭을 이루어야 하는 상황이다.
그러면 그냥 D[i] = i라는 숫자를 만들면서, 수열이 대칭인 경우의 수
라고 생각한뒤, 양 끝에 1, 2, 3이 있을테니 D[i] = D[i-1*2] + D[i-2*2] + D[i-3*2]라고 점화식을 세우고 풀면 된다.
15992번: 1, 2, 3 더하기 7
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다. 단, 사용한 수의 개수는 m개 이어야 한다.
www.acmicpc.net
M개의 숫자를 사용해야 하는 상황이다.
D[i][j] = i라는 숫자를 만들면서, j 개의 숫자를 사용한 경우의 수 라고 DP 배열을 잡은 뒤,
D[i][j] = D[i-1][j-1]+ D[i-2][j-1] + D[i-3][j-1] 이라고 점화식을 세우고 풀면 된다.
15993번: 1, 2, 3 더하기 8
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 100,000보다 작거나 같다.
www.acmicpc.net
짝수개의 숫자를 썼는지, 홀수 개의 숫자를 썼는지를 저장해야 한다.
근데, 생각해보면 어떤 숫자를 한개 더 사용하면 짝수개 -> 홀수개, 홀수개-> 짝수개 로 변한다.
따라서
D[i][j] = i라는 숫자를 만들면서 (j = 0, 짝수) or (j = 1, 홀수) 인 경우의 수라고 DP 배열을 잡은 뒤,
D[i][j] = D[i-1][(j+1)%2] + D[i-2][(j+1)%2] + D[i-3][(j+1)%2]이라고 점화식을 세우고 풀면 된다.
16195번: 1, 2, 3 더하기 9
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다. 단, 사용한 수의 개수는 m개 이하 이어야 한다.
www.acmicpc.net
7번 문제에서 푼 점화식을 가져오고, 답을 도출하는 과정에서 반복문 하나만 추가해서 이하의 경우의 수를 구하면 된다. 또한, MOD를 적용하는 것을 잊지말자.
이번 시리즈는 쉬워서, 이전 시리즈보다 먼저 끝났다...(언제 풀지)
Rmx
'내가 공부하려고 만들어가는 목록' 카테고리의 다른 글
| [내공만목] BOJ 행렬 곱셈 순서 시리즈를 풀고 싶었다.(WIP) (0) | 2020.10.30 |
|---|---|
| [내공만목] BOJ 트리와 쿼리 시리즈를 풀고 싶었다.(WIP) (0) | 2020.10.26 |
| [내공만목] 대충 어린이날에 푼 골드 문제들 정리 (0) | 2020.05.05 |
| [내공만목] 어쩌다가 knapsack 문제들을 풀게 되었다. (0) | 2020.05.03 |
| [내공만목] Convex Hull 공부하기 (0) | 2020.05.01 |