[이것 또한,,, 풀고 있는 중 정리하면서 올리고 있습니다..]
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
18236번: 행렬 곱셈 순서 2
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 263-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 263-1보다 작거나 같
www.acmicpc.net
18237번: 행렬 곱셈 순서 3
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 263-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 263-1보다 작거나 같
www.acmicpc.net
행렬 곱셈 순서 시리즈는 위에 3문제이다.
일단, 1번은 그냥 간단한 DP다.
time complexity가 O(n^3)인데..아무튼, 그냥 된다.
문제는 이제 2번과 3번인데, 사실상 2번을 풀면 3번도 풀 수 있으니 2번을 푸는 것을 목표로 삼았다.
이 미친 시리즈는 1번은 골드 3인데 2번부터 루비 3인 극한의 난이도 차이를 보인다.
아무튼, 이 시리즈에 대한 사전 지식은 아래와 같이 조금씩 모아놓았었다.
en.wikipedia.org/wiki/Matrix_chain_multiplication
Matrix chain multiplication - Wikipedia
Matrix chain multiplication (or Matrix Chain Ordering Problem, MCOP) is an optimization problem that can be solved using dynamic programming. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices. The problem i
en.wikipedia.org
www.cs.ust.hk/mjg_lib/bibs/DPSu/DPSu.Files/0211028.pdf
www.cs.ust.hk/mjg_lib/bibs/DPSu/DPSu.Files/0213017.pdf
첫번째 위키 문서에서 More efficient algorithms 부분을 보면 위 링크의 두 논문 내용을 소개하고 있다.
Hu-Shing Algorithm인데, 1번 문제를 푸는 방법과 달리 시간복잡도가 O(nlgn)이다. n^3이 nlgn으로 줄어드는 매직..
일단 위키의 내용을 해석해보자.(해석이 매끄럽지 않을 수도..)
An algorithm published in 1981 by Hu and Shing achieves O(n log n) computational complexity.
> 1981년에 Hu와 Shing이 발표한 이 알고리즘은 O(n log n) 시간 복잡도를 가진다.
They showed how the matrix chain multiplication problem can be transformed (or reduced) into the problem of triangulation of a regular polygon.
> 그들은 matrix chain multiplication problem이 정다각형을 삼각형으로 분할하는 문제로 바꾸어질 수 있음을 보였다.
The polygon is oriented such that there is a horizontal bottom side, called the base, which represents the final result.
> 정다각형은 base라 부르는 맨 아랫부분이 최종 결과값을 나타내도록 위치한다.(방향을 잡는다.)
The other n sides of the polygon, in the clockwise direction, represent the matrices.
> 정다각형에서 base를 제외한 나머지 n개의 변(간선)은 시계방향 순서대로 주어진 행렬들을 나타낸다.
The vertices on each end of a side are the dimensions of the matrix represented by that side.
> 변마다 각 끝에 있는 꼭짓점(정점)은 해당 선분으로 나타낸 행렬의 차원을 의미한다.
// 1 x 2, 2 x 3, 3 x2 행렬이 순서대로 주어진다면, 각 꼭짓점에 시계방향 순서대로 1 2 3 2 를 적어놓는다는 뜻이다.
With n matrices in the multiplication chain there are n−1 binary operations and Cn−1 ways of placing parentheses, where Cn−1 is the (n−1)-th Catalan number.
> n개의 행렬의 the multiplication chain(이제 그냥 체인이라 하겠음.)에서는 n-1개의 이항 연산(여기서는 곱셈)이 있어야 하며, C_(n-1)개의 괄호 배치 방법이 존재한다.(Cn = n번째 카탈란 수, 카탈란 수는 따로 찾아보시길..)
The algorithm exploits that there are also Cn−1 possible triangulations of a polygon with n+1 sides.
> (그래서) 이 알고리즘은 n+1면의 다각형을 삼각형으로 나누는 경우의 수는 Cn-1개라는 점을 이용한다.
This image illustrates possible triangulations of a regular hexagon.
이 이미지(위키에서 확인)는 정육각형에서 가능한 삼각형으로 분할하는 방법들을 표현한 것이다.
These correspond to the different ways that parentheses can be placed to order the multiplications for a product of 5 matrices.
> 이 방법들은 5개의 행렬을 곱셈하는 순서를 괄호를 어떻게 배치하는지에 따라 다른 것을 나타낸 것이라 볼 수 도 있다.
예시부분 생략.
[출처] WIKIPEDIA - Matrix Chain Multiplication(https://en.wikipedia.org/wiki/Matrix_chain_multiplication)
일단, 위키의 정리된 내용을 최대한 간단하게 말하면
"행렬을 간선으로 보고! 행렬의 차원을 정점으로 본 뒤에,
최종 결과값을 맨 아래 간선으로 두고 생각해보자..
그렇게 되면 n + 1 다각형을 삼각형으로 나눌 건데, 뭐가 최소 Cost일까를 찾아내면 된다."
인 것 같다.
대충 기본 아이디어에서는 감을 잡았다.
근데, 문제는 이거다.
"그래서 어떻게 하는데?"
이제 논문을 다시 차근 차근 읽어보자..
일단, PART I 논문을 읽어보면, 큰 내용은 없던 느낌이다.(내가 원하는 곳을 긁어주지는 않았다.)
결론 또한,
Based on these Therems an O(n) algorithm for finding near-optimum can be developed[12]. The cost of the partition produced by the heuristic algorithm never exceeds 1.155 Copt, where Copt is the optimum cost of partitioning the polygon. An O(n log n) algorithm for finding the unique lexicographically smallest optimum partition will be presented in Part II [13].
라고 밝혀져 있는데, 내가 원하는 것은 정확한 해이지 근사해가 아니기 때문에 part II까지 읽어야한다는 것이다... 이런 젠장
일단...그래도 PART II를 제대로 읽으려면 PART I 내용이 필요하니 한번 정리해보자.
1. Introduction
위의 위키에서 밝힌 내용과 동일하다. 따지자면 해당 알고리즘의 시간복잡도가 언급되고 있긴 한데, 넘기겠다.
2. Partitioning a convex polygon.
p.363에서 주어진 FIG.1 그래프를 보자.
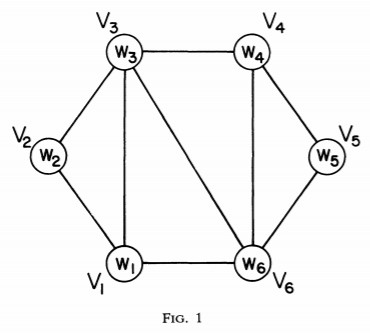
해당 그래프에서, 각 정점 Vi 마다 wi라는 것이 있다고 정의했다.
1) "이때, 이 그래프에서 도출되는 result는 w1*w2*s3 + w1*w3*w6 + w3*w4*w6 + w4*w5*w6이 나올 것이다." 임을 밝히고 있다. 왜? 다각형을 삼각형으로 쪼개고, 삼각형의 꼭짓점이 행렬의 한 차원일 때, 삼각형의 꼭짓점에 있는 값을 곱한게 연산횟수니까..!
2) V1 - V6을 이은 가장 아래 수직선을 base라고 하겠다. 다른 모든 엣지들은 base를 시작으로 시계방향으로 순서를 매기겠다.
라는 내용들이 설명글로 쭉 있고, 아래 LEMMA 1이 나온다.
LEMMA 1. Any order of muliplying of n - 1 matrices correspons to a patition of an n-gon.
지금까지 당연시하게 이야기 한 내용이다.
Proof는 직접봐도 될 듯하고, 딱히 안봐도 문제는 없음.
LEMMA 2. The minimum numbers of operations needed to evaluate the following matrix chain products ar identical.
M_1 x M_2 x ... x M_(n-2) x M_(n-1),
M_n x M_1 x ... x M_(n-3) x M_(n-2),
...
M_2 x M_3 x ... x M_(n-1) x M_n, where M_i has dimension w_i x w_(i+1) and w_(n+1) ≡ w_1.
위의 수식에서 나타난 행렬 곱셈들의 최소 연산 횟수가 모두 같다는 내용이다.
일단 생각해보면, 저기서 M_i들을 w_i로 치완해보면 모든 구성요소는 w_1부터 w_n이고, 순환된다.
따라서, 위의 그래프 형태로 나타냈을 때, 순서만 지켜지고 끝과 끝이 연결되도 문제없다는 내용이다.
행렬만으로 생각하면 왜 그런지는 모르겠지만, 생각해보면 현재 지금 행렬 곱셈 상황을 다각형의 삼각형 분할 문제로 치환했고, 그 다각형이 회전한다고 해서 result가 다르면 이슈가 있으니 당연한 이야기인것 같긴하다.
LEMMA 3. In any partition of an n-gon, n ≥ 4, there are at least two triangles, each having a vertex of degree two. (For example, in Fig 1, the triagele V_1V_2V_3 has vertex V_2 with degree 2 and the triagle V_4V_5V_6 has vertex V_5 with degree 2.)
일단, 어떤 vertex의 degree는 해당 vertex에 연결된 edge 개수라고 생각하면 된다.
그렇다면 여기서 말하는것은 적어도 4개의 정점을 가진 n-gon에서, 적어도 2개의 삼각형이 차수(degree)가 2인 정점을 한개 가지고 있다는 것이다..
증명을 봐도 좋고, 한번 그림을 그려봐도 좋다. 무조건 양끝에 있는 삼각형이 해당 성질을 가지게 되고 그건 무조건 2개일 것이다.
LEMMA 4. Let P and P' both be n-gons where the corresponding weights of the vertices satify w_i <= w_i'. Then the cost of an optimum partition of P is less than or equal to the cost of an optimum partition of P'.
증명은 생략되어있다.
만약 C(w_1, w_2, ... , w_k) 가 k-gon의 최적해를 의미한다면, 위의 LEMMA 4는 다음과 같이 나타낼 수 있다.
C(w_1, w_2, ... , w_k) <= C(w_1', w_2', ... , w_k') if w_i <= w_i'
아무튼, 그렇고.
이제, Tie-breaking-rule을 소개한다.(어떤 weight가 같은 정점들에 대해서 적용할 룰이다.)
(~2020.11.03)
'내가 공부하려고 만들어가는 목록' 카테고리의 다른 글
| [내공만목] BOJ 1, 2, 3 더하기 시리즈를 풀고 싶었다. (0) | 2020.11.03 |
|---|---|
| [내공만목] BOJ 트리와 쿼리 시리즈를 풀고 싶었다.(WIP) (0) | 2020.10.26 |
| [내공만목] 대충 어린이날에 푼 골드 문제들 정리 (0) | 2020.05.05 |
| [내공만목] 어쩌다가 knapsack 문제들을 풀게 되었다. (0) | 2020.05.03 |
| [내공만목] Convex Hull 공부하기 (0) | 2020.05.01 |