Half Adder (회로로 덧셈을 하자!)
오직 두 비트의 덧셈을 위한 회로
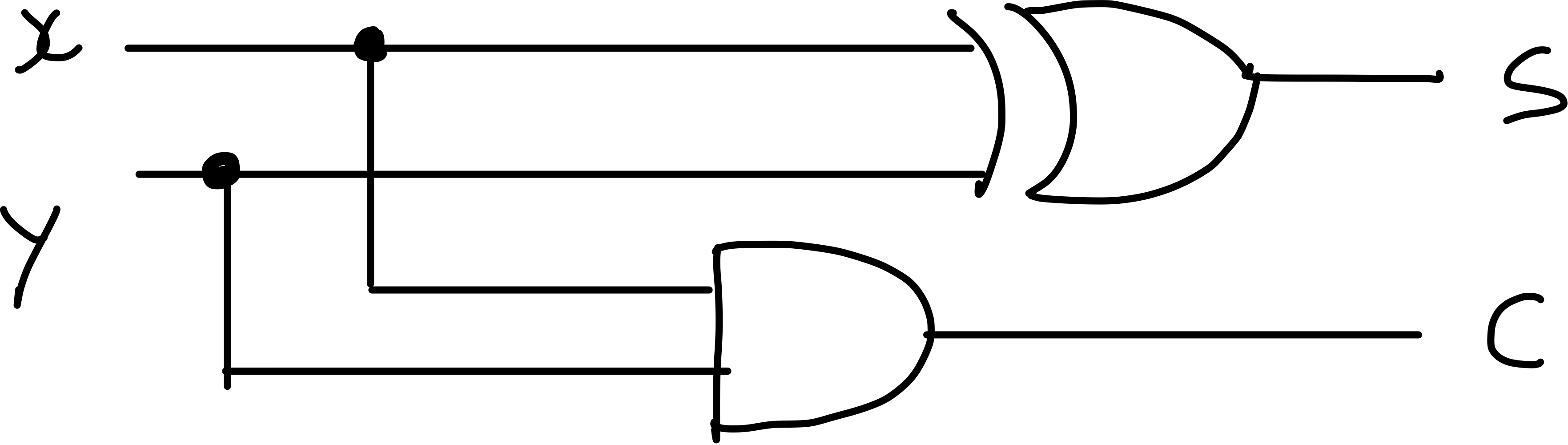

Addition of Multi-Bit Unsigned Numbers
여러 비트의 숫자를 더해볼까?
진리표를 보면... 너무끔찍하고, 이를 직접적으로 게이트로 나타내면 지수적으로 증가하는 게이트 개수를 볼 수 있다.
→ 아, 그러면 Half Adder를 계속 붙여서 여러 비트의 덧셈을 구현하자!
→ 근데, 여러개를 붙이려 하니, Carry가 발생하고, Half Adder로만은 구현이 안된다.
Full Adder
Carry를 포함해, 3개의 비트의 덧셈을 구현할 수 있다.
- Sum = x XOR y XOR ci
- Carry = xy + xci + yci
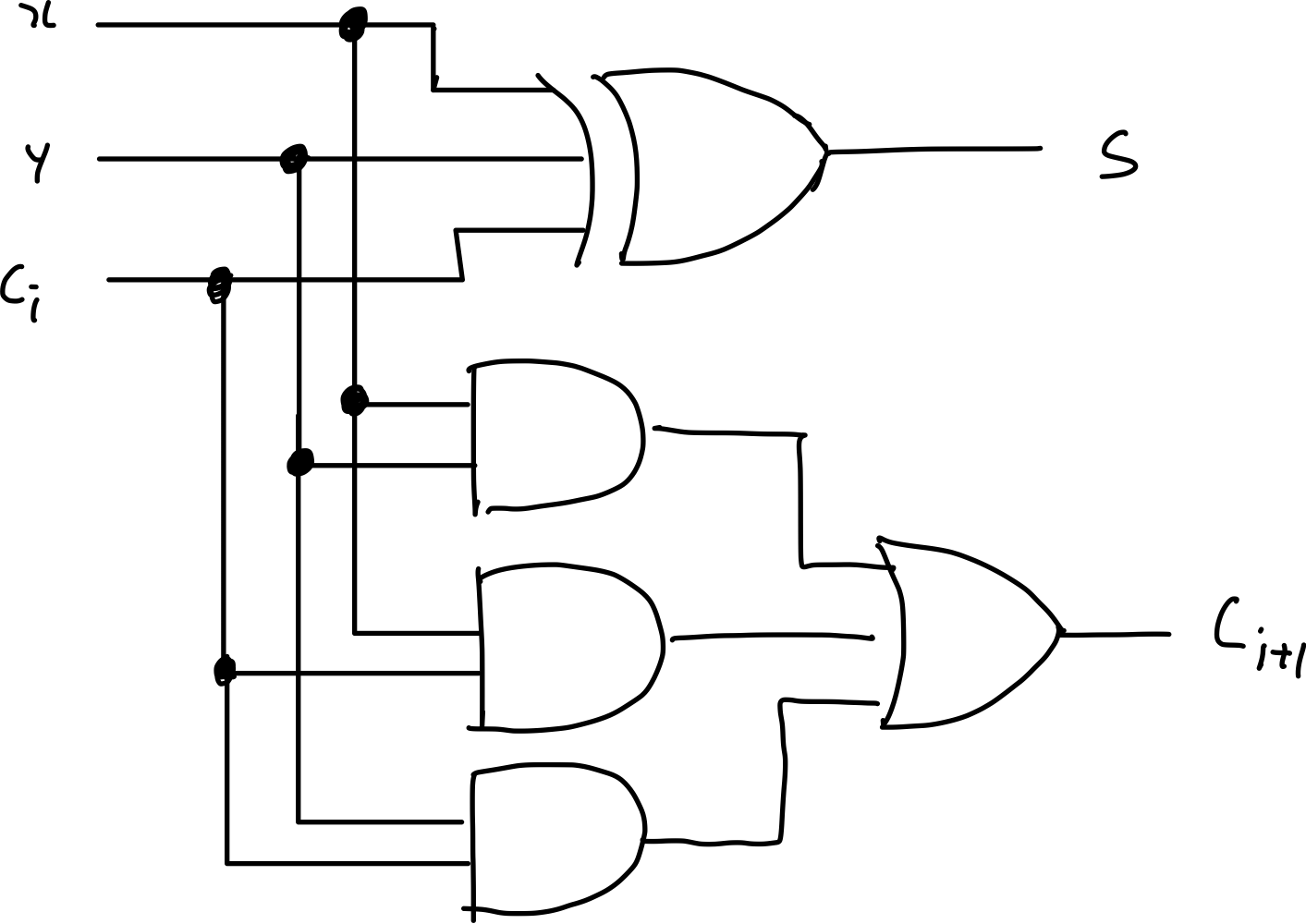

여기서 추가적으로 알 수 있는 내용!
→ XOR에 여러 개의 입력이 들어온다면, 입력의 true 개수가 홀수이면 true를 반환한다.
Carry-Ripple-Adder
(Full adder를 통해 Carry를 포함한 비트 덧셈을 만들었으니 활용해보자)
- Full-adder를 계속 연결하면 여러 비트 덧셈기를 구현할 수 있다.
- 각 열의 Carry-Out을 다음 자리의 입력으로 연결하면서 만든다.
-그러면? 크기에 상관없이 덧셈기 구현이 쉽다. 왜? 그냥 Full Adder를 연결만 하면 되니까.

근데, 이 Carry-Ripple-Adder는 문제가 있다.
모든 Carry가 전달되는 시간이 가기 전에는 틀린 답이 전달될 수도 있다. 그렇기 때문에 무조건 Carry가 다 올라가는 시간을 기다려야한다는 단점이 있다.
그래서, 이 Carry-Ripple-Adder는 사용되지 않는다.
그럼 어떻게 해결할 수 있을까?
→ Carry는 입력들만 준비되면 예측 가능하다!라는 사실을 활용하자.
→ Carry-Lookahead Adder!!를 실제로 사용한다.
Design Example: Multiply by 3
양수 3을 곱하는 회로를 설계해보자
→ A*3 = A + A + A라는 것을 활용해보자
→ Adder를 2번 쓰면 되지?
→ 근데 ,이건 좀..그렇다... SHIFT 연산을 활용해보자
→ A << 1 = A * 2이다.
그러면, (A << 1) + A를 하면 A*3을 구할 수 있다.
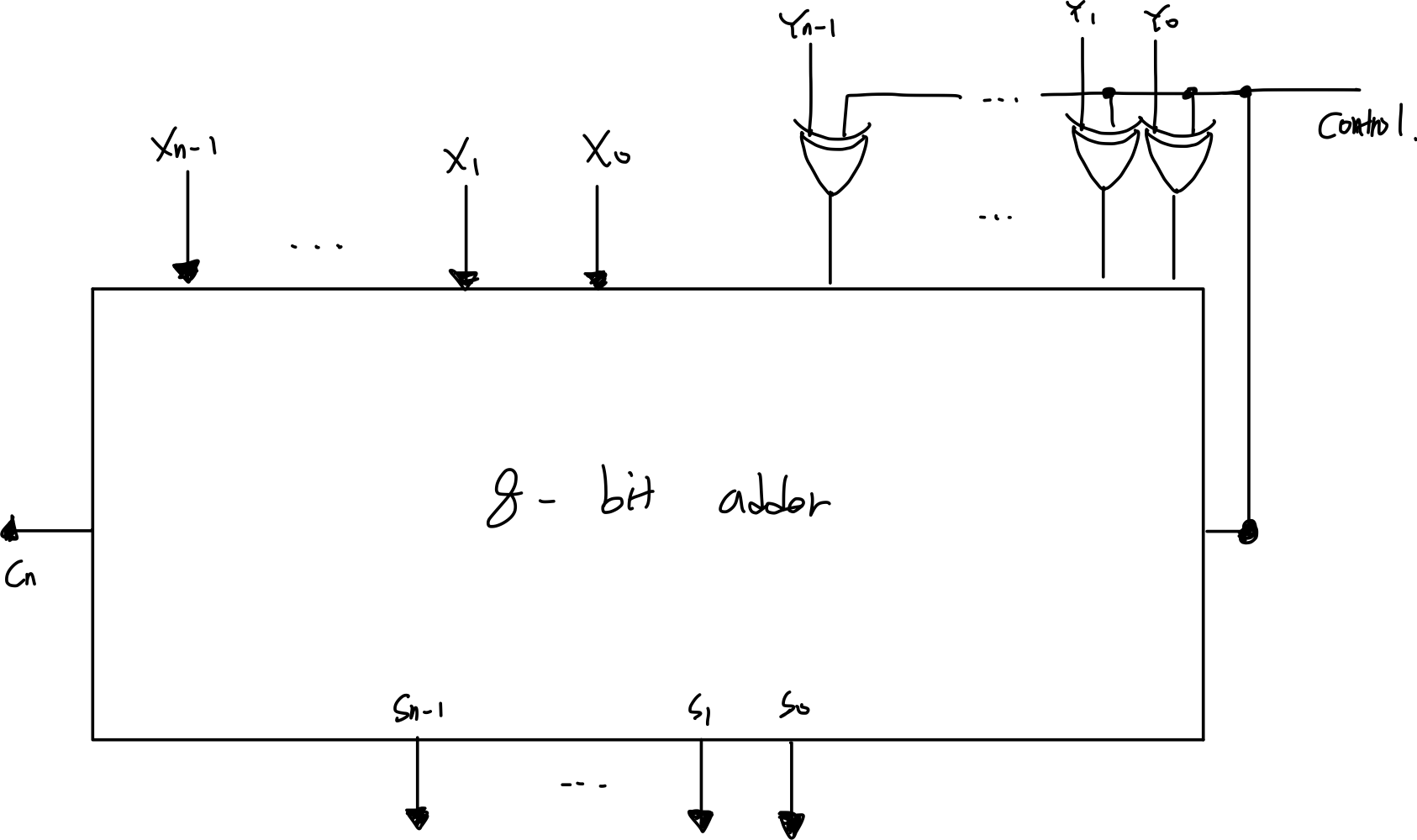
뺄셈기
- 뺄셈기는 없어..덧셈을 활용할 뿐
- 덧셈 = X + Y
- 뺄셈 = X + Y' + 1
- 2의 보수를 활용하자 -> XOR 게이트를 사용할 것이다
'KMU > 논리회로설계' 카테고리의 다른 글
| [논회설] 논리회로설계 강의 요약해보기 09-1 (0) | 2020.05.14 |
|---|---|
| [논회설] 논리회로설계 강의 요약해보기 08-1 (0) | 2020.05.13 |
| [논회설] 논리회로설계 강의 요약해보기 06-2 (0) | 2020.05.13 |
| [논회설] 논리회로설계 강의 요약해보기 06-1 (0) | 2020.05.13 |
| [논회설] 논리회로설계 강의 요약해보기 05-2 (0) | 2020.05.04 |